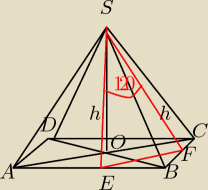
Pole powierzchni bocznej ostrosłupa prawidłowego czworokątnego jest równe 44 cm/2 , a miara
kąta między wysokościami sąsiednich ścian bocznych poprowadzonymi z wierzchołka ostrosłupa 120
stopni. Oblicz objętość ostrosłupa.
Pole powierzchni bocznej ostrosłupa prawidłowego czworokątnego jest równe 44 cm/2 , a miara
kąta między wysokościami sąsiednich ścian bocznych poprowadzonymi z wierzchołka ostrosłupa 120
stopni. Oblicz objętość ostrosłupa.
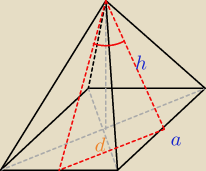 1) Ostrosłup prawidłowy czworokątny ... posiada kwadrat w podstawie
2) Wszystkie ściany boczne są jednakowe i są to trójkąty równoramienne
3) Wysokości tych trójkątów są jednakowe
4) Wysokość ściany bocznej, dzieli podstawę tegoż trójkąta (czyli bok podstawy ostrosłupa) na
pół
Pb = 4*PΔ = 44cm2 ⇔ a*h = 22
1) Ostrosłup prawidłowy czworokątny ... posiada kwadrat w podstawie
2) Wszystkie ściany boczne są jednakowe i są to trójkąty równoramienne
3) Wysokości tych trójkątów są jednakowe
4) Wysokość ściany bocznej, dzieli podstawę tegoż trójkąta (czyli bok podstawy ostrosłupa) na
pół
Pb = 4*PΔ = 44cm2 ⇔ a*h = 22
| a√2 | ||
d = √(a/2)2 + (a/2)2 = | ||
| 2 |
| d | a√2 | ||
= | |||
| 2 | 4 |
|
| √3 | ||||||||||||||||
sin 60o = | = | = | ||||||||||||||||
| h | h | 2 |